El experimento de la doble rendija, parte II
 |
| Imagen de Luis.avila.epr para Wikimedia Commons: https://es.m.wikipedia.org/wiki/Archivo:Paradoja_de_el_gato_de_Schr%C3%B6dinger.jpg |
En el post anterior hablé de cómo la reformulación del experimento de la doble rendija permitió demostrar la aparente doble naturaleza de la luz. Ahora es el momento de entrar en detalles, partiendo precisamente de nuestro último resultado.
Recordemos que al introducir un aparato de observación en el sistema, alteramos radicalmente el resultado. Este fenómeno dio lugar a que surgiesen diversas interpretaciones de la mecánica cuántica, dado que, aunque todos los resultados observados experimentalmente pueden ser descritos matemáticamente sin ningún problema, aún no disponemos de un marco "racional" para comprender exactamente el significado más profundo de la mecánica cuántica.
¿A qué me refiero con esto?
La función de onda
Bien, lo que nos demuestran las matemáticas es que cada uno de estos fotones del experimento puede ser satisfactoriamente descrito por una función matemática que abarca todo el espacio y que tiene diferentes valores en cada punto de este. Digamos, para simplificar, que cada uno de estos valores representa la probabilidad de encontrar al fotón en ese punto concreto, en un momento concreto.
El hecho de que esta función sea dependiente del tiempo implica que estos valores no son estáticos, sino que oscilan, tal y como lo haría una onda.
Imaginemos de nuevo el primer experimento, aquel en el que no se llevaba a cabo ninguna medición. La partícula liberada sería descrita matemáticamente como una onda de probabilidades, que se extiende en todas las direcciones (una onda esférica).
Para verlo fácil, observemos la función de onda desde arriba en el momento del disparo:
 |
| Esto es solo una aproximación gráfica para entender el sentido matemático de la función de onda. |
El cañón dispara una partícula, y calculamos la función de onda para solo unos instantes después del disparo, pongamos t= (100c)-1. Como es natural, vemos que hay un 75% de probabilidades de que la partícula siga una trayectoria recta y acabe en el punto más adelantado del frente de ondas. También vemos que, aunque es posible que la trayectoria se desvíe un poco, hay muy pocas probabilidades de que la partícula se desvíe 180º; y desde luego es imposible que la partícula acabe detrás del cañón y otras trayectorias similares¹.
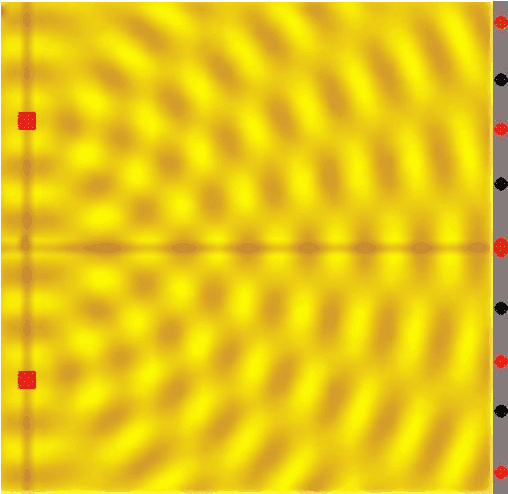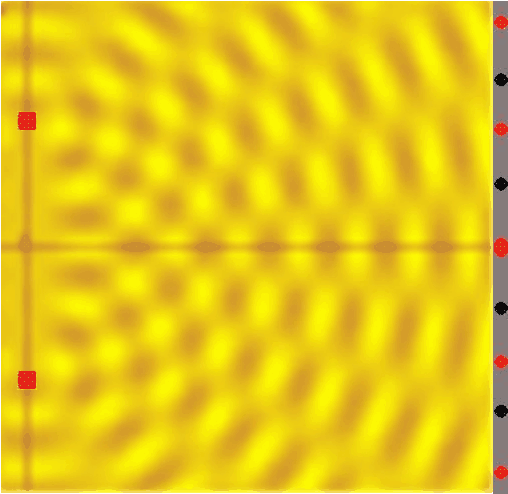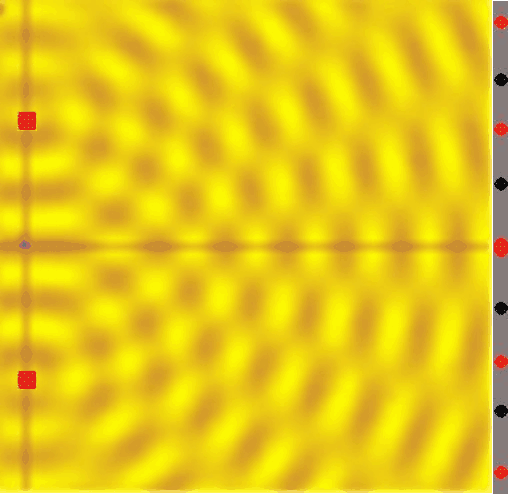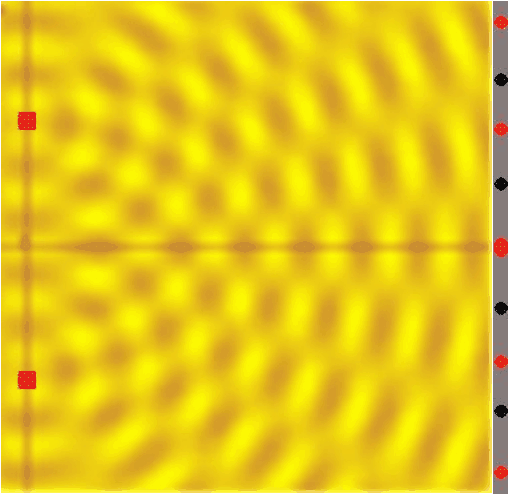
Ahora imaginemos la partícula en el instante en que se encuentra en la posición del muro de la doble rendija. Encontraremos que la función de onda nos dice que existen muchas posibilidades de que la partícula haya rebotado en el muro (por poner un número: 80% ), unas pocas de que la partícula haya atravesado la rendija izquierda (10%) y, como es natural, exactamente las mismas de que haya atravesado la rendija derecha (10%). Entonces, matemáticamente hablando, la función de onda ha "atravesado" ambas ranuras. Por eso de ese punto en adelante, cuando se calcule la función de onda, se verá que esta ha interferido consigo misma, como ya vimos anteriormente:
Por último, imaginemos el cálculo de la función de onda en el instante en el que ha atravesado ya la pantalla: ¡tendremos posibilidades reales de que la partícula se encuentre en cualquiera de los puntos rojos de la derecha!, y lo que es aún más increíble ¡es imposible encontrar una sola partícula en los puntos negros, pues las probabilidades se han hecho cero con la interferencia!
Ahora llegará la incredulidad y la frustración de muchos: "la función de onda es un objeto matemático sin relación alguna con la realidad, pues predice un patrón de interferencia porque se está ignorando una consecuencia lógica indefectible: la partícula solo puede atravesar una de las dos rendijas, por lo que, si la probabilidad no es 0% tras una de ellas, debe serlo en la otra."
¡Ya! Muy bien dicho, pero...
 |
| Imagen de Lienzocian para Wikimedia Commons: https://es.m.wikipedia.org/wiki/Archivo:Difracci%C3%B3n_de_doble_rendija.jpg |
Resulta que experimentalmente se comprueban los resultados predichos por este "objeto matemático" que es la función de onda. De hecho, se trata de un experimento repetido hasta la saciedad, que podrías hacer fácilmente en tu casa con un láser, un hilo y celofán.
¿Entonces qué es lo que está sucediendo? ¿La función de onda refleja la naturaleza dual de la luz o es solo un método matemático que nos permite conocer la evolución de un sistema aun sin entender realmente lo que está sucediendo?
Pero antes de nada, aún nos queda una cosa por entender.
El rol de la medición
Y llegamos así a la recta final del experimento, con la introducción del cuarto elemento: el aparato de medición. Recordemos que al intentar medir la posición de las partículas, estas se mostraban como partículas puntuales bien definidas, no interferían entre sí y no generaban un patrón de interferencia.De alguna forma la mera observación del fenómeno alteraba su resultado.
Voy a echar mano del otro famoso experimento de la mecánica cuántica: el gato de Schrödinger.
Se trata de un experimento mental muy esclarecedor, pero como el original habla de desintegración y otras cosas que no hemos tratado aquí, voy a adaptarlo al caso que tratamos.
Pongamos que existe una caja opaca e infranqueable, completamente cerrada, en la que se encuentra un gato.
Además, también hay un cañón de fotones. El cañón está diseñado de forma que, al disparar un único fotón, su función de onda exhiba un 50% de probabilidades de que la partícula acabe en el punto A y un 50% de probabilidades de que acabe en el punto B. Ambos puntos son interruptores lógicos, de forma que si se activa el A, pero no el B: el gato muere; si se activa el B, pero no el A: el gato sobrevive.
El famoso cuento narra cómo, mientras la caja permanezca cerrada, la partícula se encontrará en ambos interruptores, o en ninguno a la vez, pero mientras no introduzcamos un elemento de medición (como hicimos con la doble ranura), no se concretaría en ninguna de las dos posiciones. Por lo tanto, mientras la caja esté cerrada, el gato está tan vivo como muerto; sin embargo, en cuanto la abramos, veremos que el gato está o bien vivo, o bien muerto.
Sucede aquí lo que se denomina decoherencia: cuando se observa el experimento, dejan de exhibirse efectos cuánticos. Pero, ¿por qué?
En el experimento de la doble rendija, cuando introducíamos un elemento de medición, el patrón de interferencia desaparecía, y en su lugar aparecía un patrón provocado por partículas. ¿Por qué?
Al medir con nuestro aparato, estábamos interfiriendo en el experimento. La función de onda dejaba de mostrar distintas posibilidades y pasaba a mostrar que en todos los puntos del espacio la probabilidad de encontrar la partícula era 0%, salvo en uno, donde era 100%: es decir, dejábamos de tener una "onda" de distintas probabilidades, que podía difractarse e interferir consigo misma, y pasábamos a tener una partícula, que, evidentemente, no se difractaba ni provocaba interferencia alguna porque no podía "atravesar ambas rendijas" como sí lo hacía la "onda" de probabilidades.
Esto sucede porque medir significa necesariamente interaccionar con el experimento. Quizá esto no sea intuitivo (así que lo voy a simplificar para que no haya problemas) porque estamos acostumbrados a que describir una posición sea tan sencillo como establecer un punto de referencia y describir la distancia desde el punto hasta el objeto, bien fácil. Solo necesitamos un punto de referencia, que puede ser cualquiera, una unidad de medida, que se escoge en función de la escala, y conocer la posición del objeto. Evidentemente para conocer la posición del objeto tenemos que saber dónde está, tenemos que verlo. Pensemos no ya en el hecho de medir, sino en el simple hecho de ver. Nosotros podemos ver objetos, bien porque emiten luz, o bien porque la reflejan. No podemos ver a oscuras, tenemos que iluminar el objeto. Pero, ¿qué pasa si el objeto que queremos ver es un fotón? ¿si el objeto que queremos ver es luz? Os haréis una idea de hasta qué punto puede afectar a una partícula elemental el ser iluminada. Es fácil ver, entonces, que, si bien iluminar una mesa con una linterna no tiene mayor trascendencia; iluminar un fotón sería algo así como lanzar un camión contra otro. La metáfora así como la explicación son, probablemente, una excesiva simplificación; pero no es necesario nada más que comprender que el hecho de medir significa interactuar con el sistema.
Entonces cuando el sistema interactúa con el entorno, deja de exhibir efectos cuánticos: ya no nos valen las probabilidades porque si lanzo una partícula contra otra, ambas van a chocar en UN punto; o lo que es lo mismo, si abro la caja el gato no puede estar en dos estados (vivo y muerto) a la vez, tiene que estar en UNO solo. Esto es lo que se conoce como decoherencia o colapso de la función de onda, y es exactamente el punto en el que una sencilla confusión pueda hacer que se malinterprete toda la mecánica cuántica. Lo veremos en el próximo artículo.
Notas a pie de página


Comentarios
Publicar un comentario